Vector3d Class
#operators

Operators for adding (+), subtracting (-), and scaling (* or /) are supported. You may also get the magnitude (length) of a vector with the # operator.

 #vector3d:set vector3d:set(number x, number y) vector3d:set(number x, number y, number z)

Change the x, y, and (optional) z axis for a vector3d. You may also manually change these values separately via direct access.

Example:
local myVector = class.vector3d(); myVector:set(1, 1.5, 2.0); -- You may also set values in a vector directly myVector.y = 10;
 #vector3d:length number vector3d:length()

Returns the length (aka magnitude) of a vector. This is the same as the # operator.

Example:
local myVector = class.vector3d(1, 2, 3); local length = myVector.length(); -- Or you can use the # operator length = #myVector;
 #vector3d:normal vector3d vector3d:normal()

Returns a normalized (vector with a magnitude of 1) copy of a vector.

 #vector3d:dot number vector3d:dot(vector3d other)

Returns the dot product of a vector against some 'other' vector.

 #vector3d:cross vector3d vector3d:cross(vector3d other)

Returns the cross product of a vector against some 'other' vector.

 #vector3d:rotateAboutX vector3d vector3d:rotateAboutX(number angle)

Returns a copy of the vector rotated around the X axis by some angle in radians (not degrees!).

 #vector3d:rotateAboutY vector3d vector3d:rotateAboutY(number angle)

Returns a copy of the vector rotated around the Y axis by some angle in radians (not degrees!).

 #vector3d:rotateAboutZ vector3d vector3d:rotateAboutZ(number angle)

Returns a copy of the vector rotated around the Z axis by some angle in radians (not degrees!).

 #vector3d:rotateAbout vector3d vector3d:rotateAbout(vector3d axis, number angle)

Returns a copy of the vector rotated around a user-specified axis by some angle in radians (not degrees!).

 #vector3d:lerp vector3d vector3d:lerp(vector3d target, number ratio)

Linearly interpolate (lerp) a vector to rotate it towards the target vector by 'ratio' amount. 'ratio' should be between 0 (no rotation) and 1 (full rotation). Linear interpolation is quicker to calculate but less accurate than spherical linear interpolation (slerp).

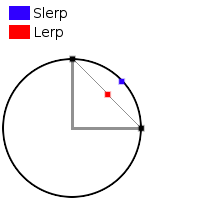
Difference between lerp and slerp

Lerp-ing will find a point that fits linearly between two other points in 3d space. On the other hand, if you were to visualize a slerp, it would track as if following the outside of a sphere. You might imagine a slerp being like the path an airplane would travel over the surface of the Earth, while lerp does not account for the curvature of the planet.

If this description doesn't seem very helpful, this video can explain the math and technical differences between the two, while this video provides a good visualization.

 #vector3d:slerp vector3d vector3d:slerp(vector3d target, number ratio)

Spherical linearly interpolate (slerp) a vector to rotate it towards the target vector by 'ratio' amount. 'ratio' should be between 0 (no rotation) and 1 (full rotation). Spherical linear interpolation is slower to calculate but is visually smoother and more accurate than linear interpolation (lerp).

For a full description on the difference between lerp and slerp, see vector3d:lerp()

 #vector3d:moveTowards vector3d vector3d:moveTowards(vector3d target, number distance)

Move this vector up to 'dist' distance towards the target vector. This will automatically prevent overstepping the target should 'dist' be longer than the actual distance to the target. If distance is negative, this function will move away from the target vector.

Page last updated at 2018-09-25 20:48:56

Copyright 2024